90^@ Given, vec P vec Q=vec R So, we can write, vec R = sqrt(P^2Q^2 2PQ cos theta),where theta is the angle between the two vectors Or, R^2 =P^2 Q^2 2PQ cos theta Given, P^2 Q^2 = R^2 So, R^2 = R^2 2PQ cos theta Or, 2PQ cos theta =0Vector R = vector P vector Q if P = Q = R, find the angle between P and Q Let P=Q=R=AMagnitude of vectorR isR=(P^2Q^22PQcosthita)where thita is angle be Book a Trial With Our Experts The magnitude of two vectors p and q differ by 1 The magnitude of their resultant makes an angle of tan inverse (3 / 4) with p The angle between p and q is

09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are
If vec p+vec q = vec p-vec q then the vectors vec p and vec q are
If vec p+vec q = vec p-vec q then the vectors vec p and vec q are-P*Q is a vector perpendicular to the plane of P and Q Now any vector in the plane of P and Q can be expressed as a linear combination of P and Q Here P Q is also a linear combination of P andShow vector (pq) is orthogonal to the curve at q Let f R → R n be a differentiable mapping with f ′ ( t) ≠ 0 for all t in R Let p be a fixed point not on the image curve of f If q = f ( t 0) is the point of the curve closest to p, that is, p − q ≤ p − f ( t) for all t in R, show that vector ( p − q




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude
Q Given that $\overrightarrow{P} \overrightarrow{Q} \overrightarrow{R} = \overrightarrow{0}$ Two out of the three vectors are equal in magnitude The magnitude of the third vector is $\sqrt{2}$ times that of the either of the other two The possible angles between these vectors will be If we have any 2 vectors P and Q, the dot product of P and Q is given by P • Q = P Q cos θ where P and Q are the magnitudes of P and Q respectively, and θ is the angle between the 2 vectors The dot product of the vectors P and Q is also known as the scalar product since it always returns a scalar value The angle between p of the resultant of pq and pq Since we know that p q and p q, lets consider that p and 2p are parallel We need to consider that a resultant vector is the double of the initial magnitude and the same direction as the first one Therefore, we can from this conclude that the angle wil be equal to 0º
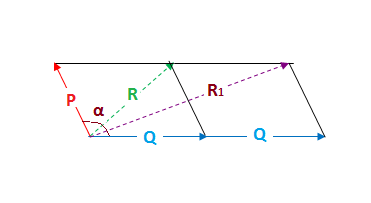
0 votes 1 answer What is the angle between P and the resultant of (P Q) and (P Q) ? Magnitude Sum of Two vectors Vector P and Vector q is given by r^2 =p^2q^22pqcos($) _____(i) here $ indicates angle between them We are given r=pq so Squaring both the sides we get r^2=p^2q^22pq _____(ii) From (i) and (ii) we can write p^2q^22pqcos($)=p^2q^22pq therefore 2pq=2pqcos($)That is AB → =p, BC → =q ⇒ AC → =pq This definition of vector addition is referred to as the triangle law of addition You can then subtract vectors, for a−b simply means a−()b For example AB → =BC → −AC → As an example, consider the displacement
Click here👆to get an answer to your question ️ The resultant of two vectors P⃗ and Q⃗ is R⃗ If Q is doubled, the new resultant is perpendicular to P Then R equalsNow if cross product of two vectors is 0 , one must a multiple of other so that crossproduct of the same vectors is 0 So , $ q3r = \lambda p $ which implies on substituting $ p \times \lambda p = \lambda p \times p = \lambda 0 = 0 $ Thus proved Share Cite Follow answered Jul 12 '16 at 603And q, then the third side, AC, is defined as the vector sum of p and q;




The Resultant Of Two Vectors P And Q Is R If The Vector Q Is Reversed Then The Resultant Becomes S Then Choose The Correct Option



What Is The Angle Between P Q And P Q Vectors Quora
8 Find the unit vector in the direction of PQ vector where P and Q are the points (1, 2, 3) and (4, 5, 6), respectivelyHow to subtract Vectors? If PQ=PQ (where P and Q are vectors) then the magnitude of vector Q is




What Is P Q And R




Solved Question 1 Vectors P Q And R Are Three Points Wi Chegg Com
Transcript Ex 102, 8 Find the unit vector in the direction of vector (𝑃𝑄) ⃗ , where P and Q are the points (1, 2, 3) and (4, 5, 6);P q p→ q ¬p∧(p→ q) ¬p∧(p→ q) → ¬q T T T F T T F F F T F T T T F F F T T T So ¬p∧(p→ q) → ¬qis not a tautology 1 3 (0 points), page 35, problem 18 p→ q ≡¬p∨q by the implication law (the first law in Table 7) ≡q∨(¬p) by commutative laws Resultant of two vectors P & Q is inclined at 45° to either of them What is the magnitude of the resultant asked in Physics by KumariMuskan (339k points) vectors;



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And




Copy Of Chapter 01
This sentence is of the form "If p then q" So, the symbolic form is p → q wherep Today is Sunday q It is a holiday Converse StatementIf it is a holiday, then today is Sunday Inverse Statement If today is not Sunday, then it is not a holiday Contrapositive StatementIf it is not a holiday, then today is not Sunday Part0211 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any of p, q is true and also when both are true On the other hand ⊕ represents an exclusive or, ie, p⊕ q is true only when exactly one of p and q is true 112That p_q!ris actually (p_q) !r, though it is far better to simply regard the statement as ambiguous and insist on proper bracketing To make a truth table, start with columns corresponding to the most




What Is P Q And R



The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Perpendicular To P Then R Is Equal To Socratic
The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Perpendicular To P Then R Is Equal To Socratic Two Vectors P And Q Are Inclined To Each Other At An Angle Of 60 Degrees The Magnitude Of P And Q Is 10 And 25 Respectively What Is The Angle Alpha2i 3j x y p 5i j q b) Express pand q using column vector notation p= 2 3 ,q= 5 1 c) By translating one of the vectors, show the sum pq on an xy plane 7i Consider the statement q For any real numbers a and b, a^2 = b^2 ⇒ a = b By giving a counterexample, prove that q is false asked in Algebra by Vikram01 ( 515k points) mathematical reasoning




Vectors P Q And R Have Magnitude 5 12 And 13 Units And P Q Is Equal To R If Angle Between Q And R Is Brainly In



Solution How Can We Show That P Q And R Are Collinear Vector Geometry Underground Mathematics
Let C be the angle between two vectors p1 and p2 The resultant R is given by the formula R^2 = (p1)^2(p2)^22p1p2cos C {√(3P^2Q^2)}^2 = (PQ)^2(PQ)^22(PQ)(PQ)cos C or, 3P^2Q^2 = P^2Q^22PQ P^2Q^22PQ 2(P^2Q^2)cos C or 2 P → Q A s s u m This second assumption is good too, since you basically want to do a DeMorgan on line 1, and to do those in Natural Deduction, you do a Proof by COntradiction on each of the disjuncts so yes, assume the disjunct, but then proceed with getting the full disjunct 3 ( P → Q) ∨ ( Q → P) ∨ I n t r o ( 2)Answer to What is the angle between the resultants of P Q and P Q where P and Q are two vectors By signing up, you'll get thousands of




If P I 2j K And Q I 4j 2k Are Position Vector P V Of Points P And Q Find The Position Vector Of The Point R Which Divides Segment Pq Internally In The Ratio 2 1 Mathematics




Given That P Q R If Pvector Qvector Rvector Then The Angle Between Pvector And Rvector Is 81 If Pvector Qvector Rvector 0 The The Angle Between Pvector And Rvector Is What Is The Relation Between 81
The vectors p, q and y are expressed in terms of the vectors t and s as follows p= 3t 2s q= 5t – s y=ht (hk)s Where h and k are constants Given that y=2p3q, find the values of h and k 5 Find the position vector of point R which divides line MN internally in the ratio 23 Take the position vectors of M and N to be Then, it can be written as, s = p – q = p ( q) Vector addition – analytical method Parallelogram law If two vectors P and Q are represented by two adjacent sides of a parallelogram both pointing outwards, then the diagonal of the parallelogram represents the resultant of P and QUsing the coplane of p → and q → that is the plane defined by vectors p and q as the coordinate plane we can restate the first equation as the projection of vector p → on vector q → is 0 using plane geometry we arrive at the conclusion that the angle between p and q θ is 90 another way to state this is that p → • q → = p q cos θ = 0 assuming the size of each vector is not 0 we are left withcthd conclusion that p and q




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube



There Are Two Positive Number P And Q Such That P Q 2 And P4 Q4 272 Find The Quadratic Equation Whose Roots Are Jee Neet Qna
If P Q = P Q, then angle between P and Q If the magnitude of differences of two vectors A and B of equal magnitudes is equal to magnitude of either of the given vectors The angle between the vectors A and B will be If the vectors, vector p = (a 1)i aj ak, vector = ai (a 1)j ak and vector r = ai aj (a 1)k (a ∈ R) are coplanar and 3(pq) 2 λ r x q 2 = 0, then(a) Zero asked in Physics by KumariMuskan (33



Three Vectors Vector P Vector Q And Vector R Are Shown In The Figure Sarthaks Econnect Largest Online Education Community




If Vector P Vector Q P Q Then The Angle Between P And Q Is Maths Vector Algebra Meritnation Com
If u,v and w are noncoplanar vectors and p,q are real numbers, then the equality 3 u p v p w p v w q u 2 w q v q u = 0 holds for If u,v and w are noncoplanar vectors and p,q are real numbers, then the equality 3 u p v p w p v w q u 2 w q v q u = 0 holds for Please log in or register to add a comment Find the angle between two vectors p and q, if p x q = pq Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, If p and q are two unit vectors and the angle between them is 60 then (1pq)/(1pq) Get the answers you need, now!




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled The New R Askiitians
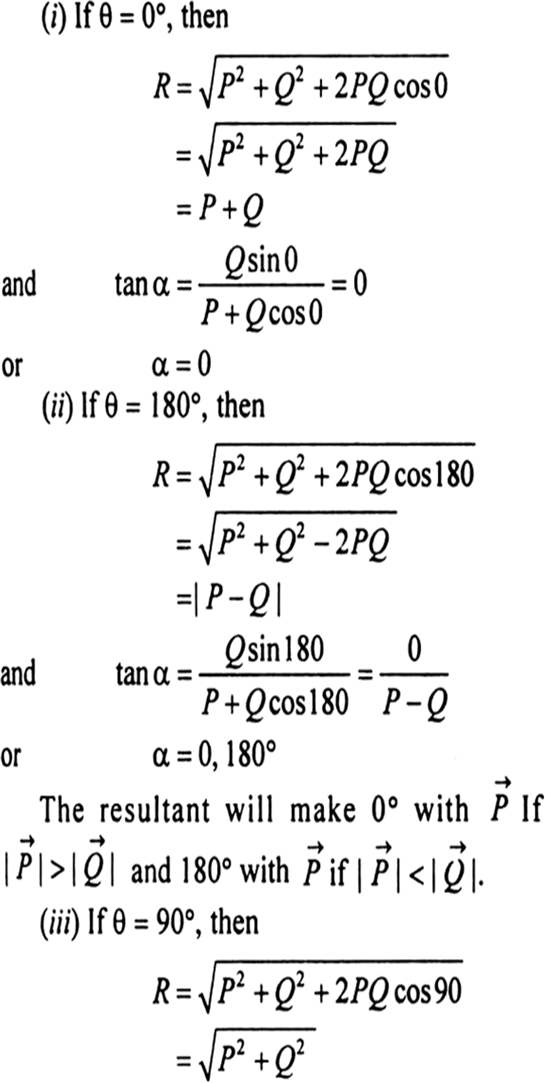



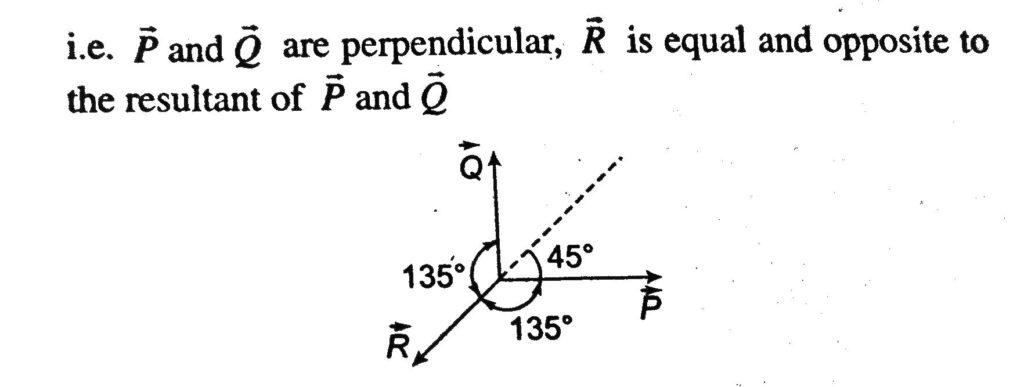
Find The Magnitude And Direction Of Resultant Of Two Vectors Analytically Discuss The Special Cases For Angle Between The Vectors I 0 Ii 180 Iii 90 From Physics Motion In A Plane Class 11 Cbse
Let two vectors P and Q be P=PxiPyjPzk and Q=QxiQyjQzk Now PQ = (PxQx)i (PyQy)jPzQz)k and PQ= (PxQx)i (PyQy)j (PzQz)k The resultant of PQ and PQ is 2 (PxiPyjPzk) which has double the length of vector P same direction as P So the angle between P and the resultant of PQ and PQ is zeroIf the vectors 3pq;5p3q and 2pq;4p2p are pairs of mutually perpendicular vectors then sin (p^q) is here i have written p and q for p bar and q bar,those are vectors,sorry for inconvience (A)√55/4 (B)√55/8 3/16 (D)√247/16 sin (p^q) means sin of angle b/w p and q please give detailed solution please helpQuestion From – DC Pandey PHYSICS Class 11 Chapter 05 Question – 043 VECTORS CBSE, RBSE, UP, MP, BIHAR BOARDQUESTION TEXTThe angles between PQ and PQ wil




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude
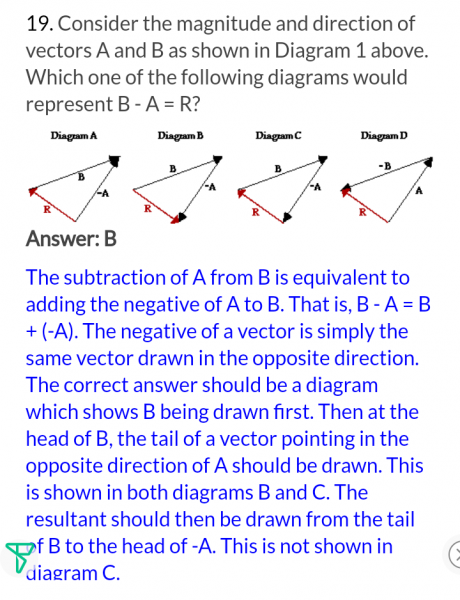



In The Above Fig Pq And R Are Vectors Which Of The Following Options Gives Myschool
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeIf the Position Vectors of P and Q Are ^ I 3 ^ J − 7 ^ K and 5 I − 2 ^ J 4 ^ K Then the Cosine of the Angle Between → P Q and Yaxis is Mathematics Advertisement Remove all ads Advertisement Remove all ads Advertisement Remove all ads MCQ Sum If vector P vector Q = vector P vector P then the angle between the vectors vector P and vector Q (a) 0° (b) 90° asked in Kinematics by AmarDeep01 ( 502k points) kinematics




If P Q 0 Then Which Of The Following Is Necessarily Ture



The Resultant Of Two Forces P And Q Is R If R Is Doubled Class 11 Maths Cbse
Explanation The form of a modus tollens argument resembles a syllogism, with two premises and a conclusion If P, then Q Not Q Therefore, not P The first premise is a conditional ("ifthen") claim, such as P implies QThe second premise is an assertion that Q, the consequent of the conditional claim, is not the case From these two premises it can be logically concluded that P,The locus of \(P\) will be the line \(x = a\), while the locus of \(Q\) will be \(x = a\) These are parallel straight lines These are parallel straight lines The diagram shows the case \(a = 2\)Subtracting a vector is the same as adding its negative The difference of the vectors p and q is the sum of p and –q p – q = p (–q) Example Subtract the vector v from the vector u Solution u – v = u (–v) Change the direction of vector v to get the vector –v



Adding Vectors Algebraically Graphically Video Khan Academy



Two Forces P 1 Dyn Q 3 Dyn And They Are In 90 Degree To Each Other What Is The Angle Between The Vectors P Q And P Q Physics Topperlearning Com
Example 11 Consider two points P and Q with position vectors (𝑂𝑃) ⃗ = 3𝑎 ⃗ − 2𝑏 ⃗ and (𝑂𝑄) ⃗ = 𝑎 ⃗ 𝑏 ⃗ Find the position vector of a point R which divides the line joining P and QVectors P Q and R have same magnitudeWhen vector P and Vector Q is added we get vector R ( using triangle law) we get a triangle PQR Now as magnitude is same it is equilateral triangle Therefore each angle is 60 degrees In triangle law head of vector P is connected to tail of vector Q But angle between two vectors is possible tail to tailRespectivelyP (1, 2, 3) Q (4, 5, 6) (𝑃𝑄) ⃗ = (4 – 1) 𝑖 ̂ (5 – 2) 𝑗 ̂ (6 – 3) 𝑘 ̂ = 3𝑖 ̂ 3𝑗 ̂ 3𝑘 ̂ ∴ Vector joining P and Q is given by (𝑃𝑄) ⃗ = 3𝑖 ̂ 3𝑗 ̂ 3𝑘 ̂ Magnitude of (𝑃𝑄



Http Onlinelibrary Wiley Com Doi 10 1002 App1 Pdf




If Vecp Vecq Pq Then Angle Between Vecp And Vecq Is
P – Q = P (Q) Multiplication of Vectors If k is a scalar quantity and it is multiplied by a vector A, then the scalar multiplication is given by kA If k is positive then the direction of the vector kA is the same as vector A, but if the value of k is negative, then the direction of vector kA will be opposite to the direction of vector A




The Position Vectors Of P And Q Are Respectively A And B If
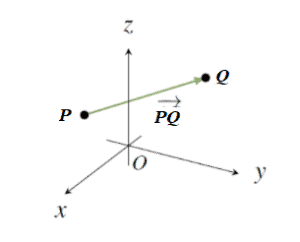



Vector Geometry Explanation And Examples



Lorentzian Causality Theory Springerlink




Autocad Vector Vba Frfly




Engen1 B 11 09 18 Lecture Notes 29 Course Engen1b Date 11 Revision Of Matrix Algebra There Is Sample Test Sample Test Put Up On Moodle For Your Revision Studocu



1



If P Q Are Real And P Q Then Show That The Roots Of The Equation P Q X 2 5 P Q X 2 P Q 0 Are Real And Unequal Sarthaks Econnect Largest Online Education Community




P Q R And P Q C Then Q Is P Q R Are Vectors




The Resultant Of Two Vectors P And Q Is R If The Magnitude Of Q Is Doubled The New Resultant Vector Becomes Perpendicular To P Then The Magnitude Of R Is Equal




Given That P Vector Q Vector R Vector And That R Vector Is Perpendicular To P Vector If P R Brainly In




Brain Wave Posts Facebook



1




Vector Questions Abbreviated Solutions



Http Citeseerx Ist Psu Edu Viewdoc Download Jsessionid A0296fd9a93c471ace81f3b31f1626 Doi 10 1 1 217 7801 Rep Rep1 Type Pdf




Let P 3 Q 3 4 And Pq 2 3 Find P Q Mathematics Stack Exchange
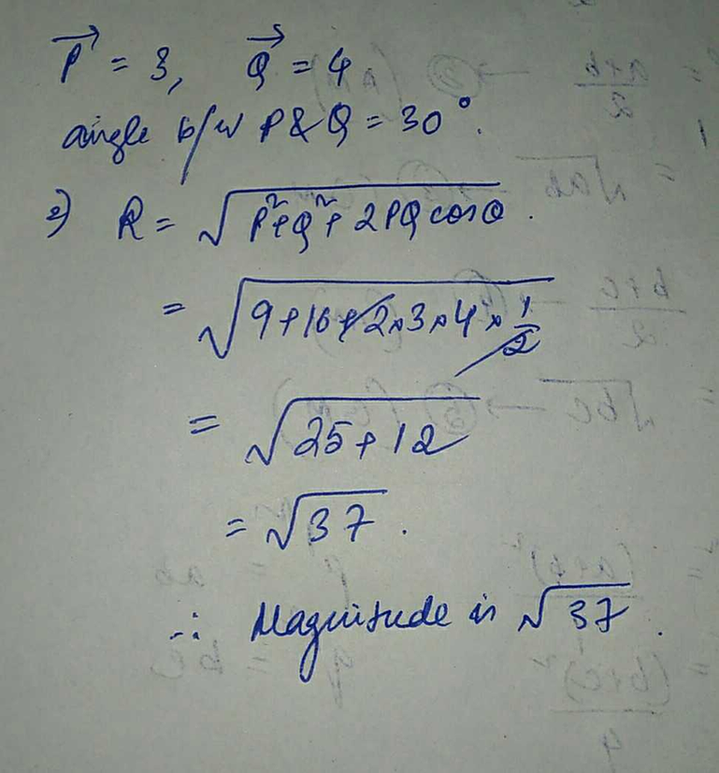



Two Vectors P And Q Have Magnitudes 3 Units And 4 Units Resp Scholr




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora
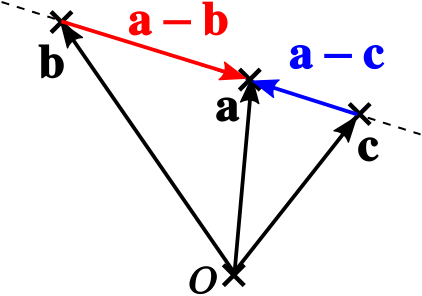



Solution How Can We Show That P Q And R Are Collinear Vector Geometry Underground Mathematics



If The Resultant Of Two Vectors P Q Is P Q Then Angle Between P Q Is Quora




Copy Of Chapter 01




If Vecp Vecq Then Which Of The Following Is Not Correct




Negative Vectors Explanation Examples




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled T Scholr



If Q Is A Point Oh The Side Sr Of A Dpsr Such That Pq Pr Then Prove That Ps Pq Studyrankersonline



P Q R And S Are Respectively The Mid Points Of The Sides Ab Cd And Da Of A Quadrilateral Abcd Such That Ac Studyrankersonline



Www Ualberta Ca Rjia Math214 Part2 Lec2a Pdf




Find The Unit Vector In The Direction Of Vector Pq Where P And Q Are



Www Jstor Org Stable



2




The Resultant Of Two Vectors P O Is If The Magnitude Of Oi Scholr




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




What Is The Angle Between P Q And P Q Youtube




Copy Of Chapter 01




Question 3 Consider The Two Position Vectors P And Q Chegg Com
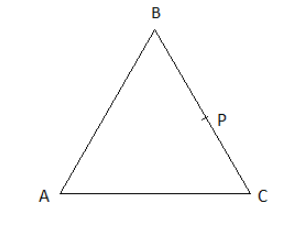



Abc Is A Triangle And P Is Any Point On If Overline Class 10 Maths Cbse




Find The Magnitude And Direction Of Resultant Of Two Vectors Analytically Discuss The Special Cases For Angle Between The Vectors I 0 Ii 180 Iii 90 From Physics Motion In A Plane Class 11 Cbse




The Resultant Of Two Vectors P And Q Is R If The Magnitude Of Q Is Doubled The New Resultant Vector Becomes Perpendicular To P Then The Magnitude Of R Is Equal



Consider Two Vectors P And Q Of Equal Magnitude If The Magnitude Of P Q Is Two Times Larger Than That Of P Q Then What Is The Angle Between Them Quora




Physics Reference Physics 9702 Doubts Help Page 151




Find Angle Between P Vector And Q Vector If Resultant Is Given By R 2 P 2 Q 2 Physics Topperlearning Com 40y2cnxx




In The Above Fig Pq And R Are Vectors Which Of The Following Options Gives Myschool




Tensor Wikipedia



O Is The Origin Op P And Oq Q Z Is A Point On Pq Such That Pz Zq 5 2 How To Work Out In Terms




C Terminal Splice Variants Of P Q Type Ca2 Channel Cav2 1 A1 Subunits Are Differentially Regulated By Rab3 Interacting Molecule Proteins Journal Of Biological Chemistry



2



1
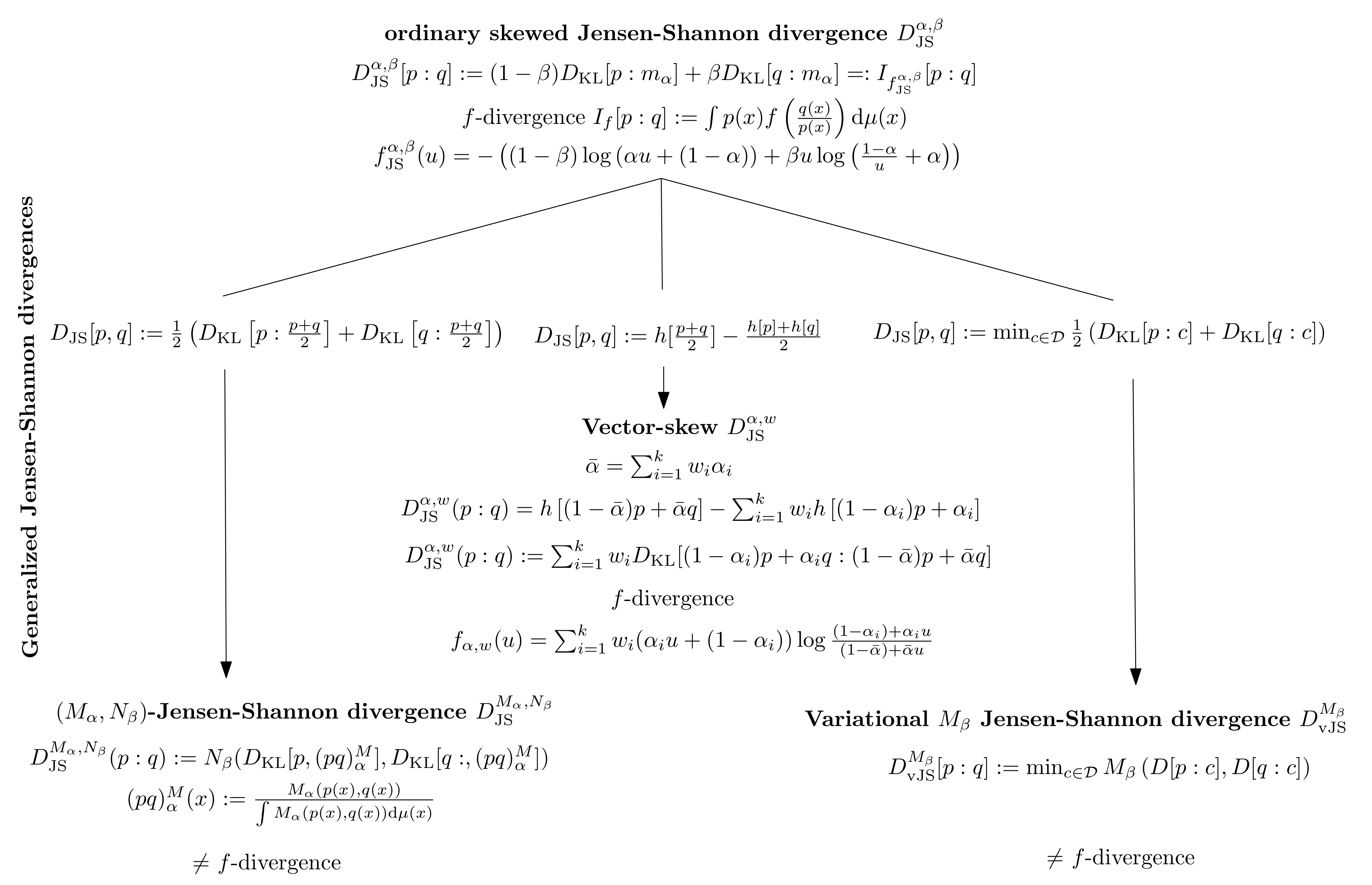



Entropy Free Full Text On A Variational Definition For The Jensen Shannon Symmetrization Of Distances Based On The Information Radius Html




8 4 Vectors A Vector Is A Quantity That Has Both Magnitude And Direction Vectors In The Plane Can Be Represented By Arrows The Length Of The Arrow Ppt Download



Link Aps Org Pdf 10 1103 Prxquantum 2




The Resultant Of Two Vectors P And Q Is Perpendicular To P And Its Magnitude Is Half Of That Of Q Brainly In




If U V W Are Non Coplanar Vectors And P Q Are Real Numbers Then The Equality Brainiak India




Magnitude And Direction Of Vectors



Solved The Magnitudes Of Vectors P Q And R Are 100 Kn 250 Kn And
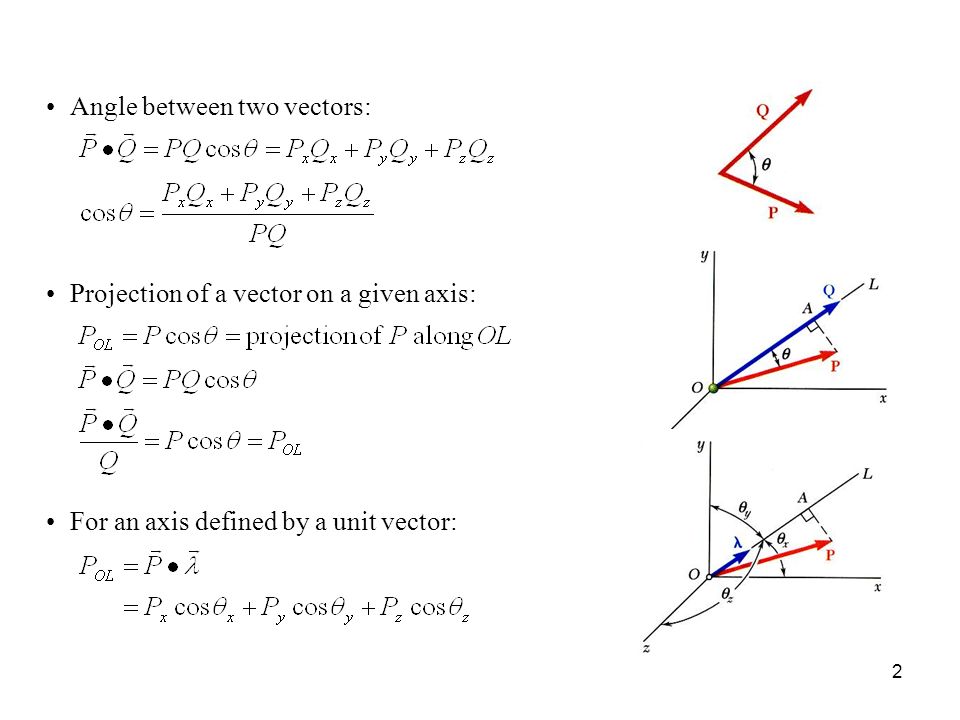



1 The Scalar Product Or Dot Product Between Two Vectors P And Q Is Defined As Scalar Products Are Commutative Are Distributive Are Not Associative Ppt Download




A The Column Vectors P And Q Are Defined By P Chegg Com




Quaternion Wikipedia




If P Q R And P Q R The Ratio Of Angles Between P And R And P And Q Physics Motion In A Plane Meritnation Com




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are




The Angles Between P Q And P Q Will Be Youtube




If P Q P Q And O Is The Angle Between P And Q Then A 0 00 B 0 900 C P 0



2




Euclidean Distance Wikipedia




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Youtube
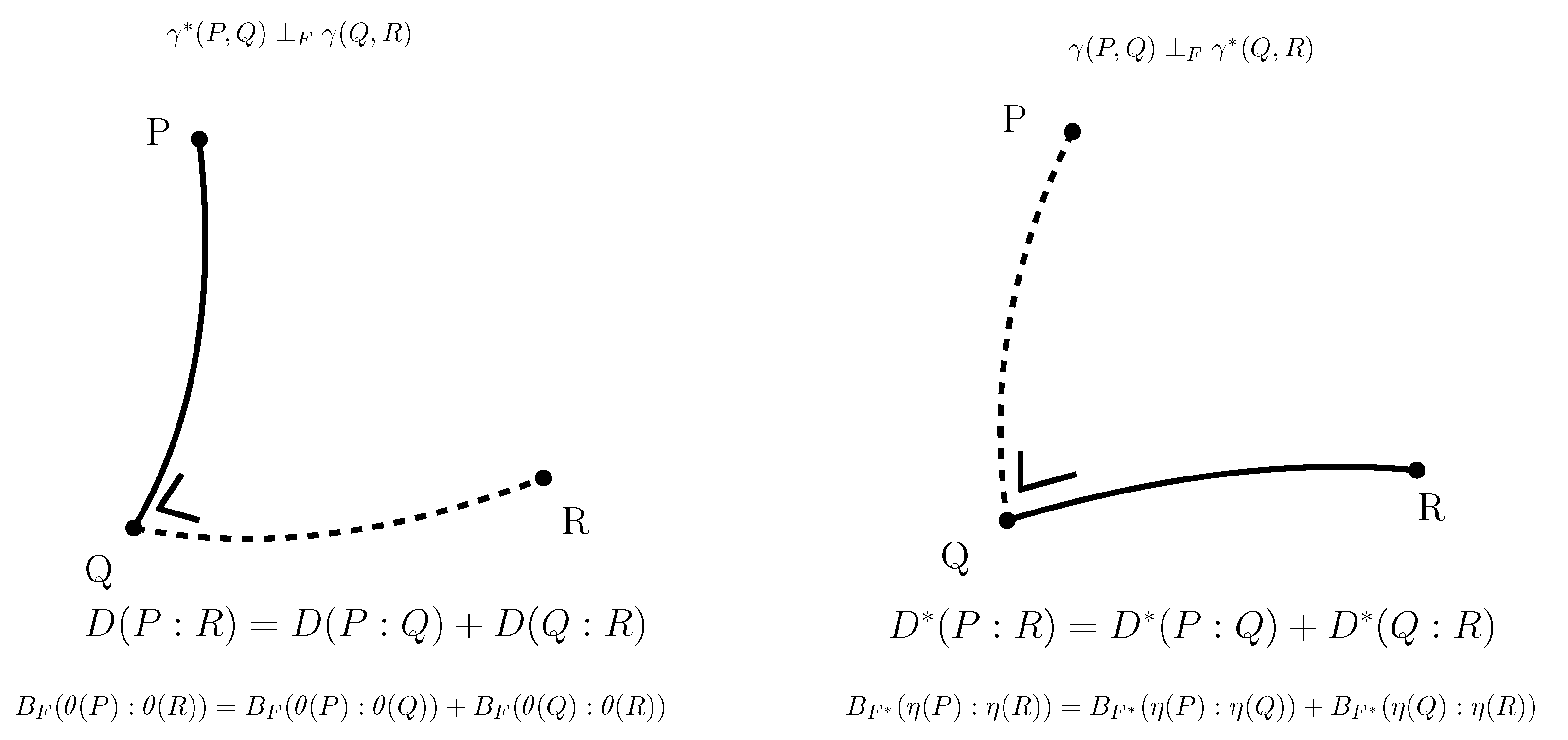



Entropy Free Full Text An Elementary Introduction To Information Geometry Html
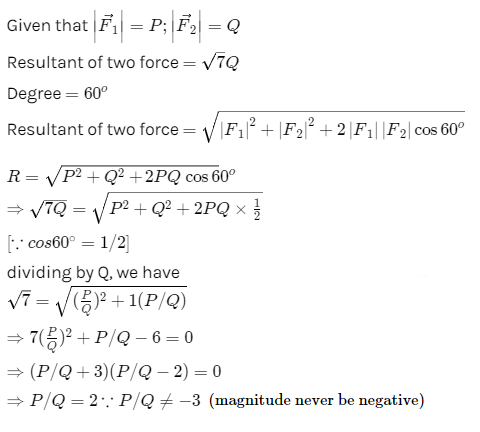



If The Resultant Of Two Forces Of Magnitudes P And Q Acting At A Poin Askiitians




If P Q P Q Then




The Angles Between P Q And P Q Will Be Youtube




1 Prove That The Empty Set Is A Subset Of Every Set Pdf Free Download




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com



Link Aps Org Pdf 10 1103 Prxquantum 2



The Sum Of Two Forces Vector P And Q Is Vector R Such That Vector R P The Angle 8 In Degrees That The Resultant Of Vector 2p And Q Sarthaks Econnect




The Position Vectors Of P And Q Are Respectively A And B



The Resultant Of The Vector P And Q Is Perpendicular To The Vector P What Is The Angle Between P And Q Quora



Vector Line And Plane Equation A Level Maths Uptuition With Mr Will




If P Vector Dot Q Vector Is Equal To Pq Then Angle Between P And Q Is Brainly In



0 件のコメント:
コメントを投稿